Electric potential is the potential energy per unit of charge associated with a static (time-invariant) electric field, also called the electrostatic potential, typically measured in volts. It is a Lorentz scalar quantity. The difference of electrical potential between two points is known as voltage.
There is also a generalized electric scalar potential that is used in electrodynamics when time-varying electromagnetic fields are present. This generalized electric potential cannot be simply interpreted as a potential energy, however.

Explanation
Objects may possess a property known as electric charge. An electric field exerts a force on charged objects, accelerating them in the direction of the force, in either the same or the opposite direction of the electric field. If the charged object has a positive charge, the force and acceleration will be in the direction of the field. This force has the same direction as the electric field vector, and its magnitude is given by the size of the charge multiplied with the magnitude of the electric field.
Classical mechanics explores the concepts such as force, energy, potential etc. in more detail.
Force and potential energy are directly related. As an object moves in the direction that the force accelerates it, its potential energy decreases. For example, the gravitational potential energy of a cannonball at the top of a hill is greater than at the base of the hill. As the object falls, that potential energy decreases and is translated to motion, or inertial (kinetic) energy.
For certain forces, it is possible to define the "potential" of a field such that the potential energy of an object due to a field is dependent only on the position of the object with respect to the field. Those forces must affect objects depending only on the intrinsic properties of the object and the position of the object, and obey certain other mathematical rules.
Two such forces are the gravitational force (gravity) and the electric force in the absence of time-varying magnetic fields. The potential of an electric field is called the electric potential.
The electric potential and the magnetic vector potential together form a four vector, so that the two kinds of potential are mixed under Lorentz transformations.

Mathematical introduction
When time-varying magnetic fields are present (which is true whenever there are time-varying electric fields and vice versa), one cannot describe the electric field simply in terms of a scalar potential φ because the electric field is no longer conservative: is path-dependent because .
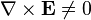Instead, one can still define a scalar potential by also including the magnetic vector potential 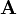. In particular, 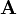is defined by:

where is the magnetic flux density. One can always find such an 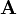because (the absence of magnetic monopoles). Given this, the quantity is a conservative field by Faraday's law and one can therefore write:

where φ is the scalar potential defined by the conservative field .
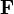The electrostatic potential is simply the special case of this definition where 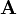is time-invariant. On the other hand, for time-varying fields, note that , unlike electrostatics.
Note that this definition of φ depends on the gauge choice for the vector potential 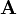(the gradient of any scalar field can be added to 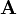without changing ). One choice is the Coulomb gauge, in which we choose . In this case, we obtain , where ρ is the charge density, just as for electrostatics. Another common choice is the Lorenz gauge, in which we choose 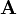to satisfy .

Special cases and computational devices
This electric potential, typically measured in volts, provides a simple way to analyze electric circuits without requiring detailed knowledge of the circuit shape or the fields within it.
The electric potential provides a simple way to analyze electrical networks with the help of Kirchhoff's voltage law, without solving the detailed Maxwell's equations for the fields of the circuit.